Dessiner un électrocardiogramme avec un shader

On se propose de dessiner une courbe d’électrocardiogramme avec un shader (GLSL). Il s’agit d’une répresentation approximative, le but n’est pas de simuler quoique ce soit mais juste de manipuler un shader.

Le code complet est disponible sur le dépôt et le résultat final ressemble à ça (la qualité est un peu dégradée par le format GIF):

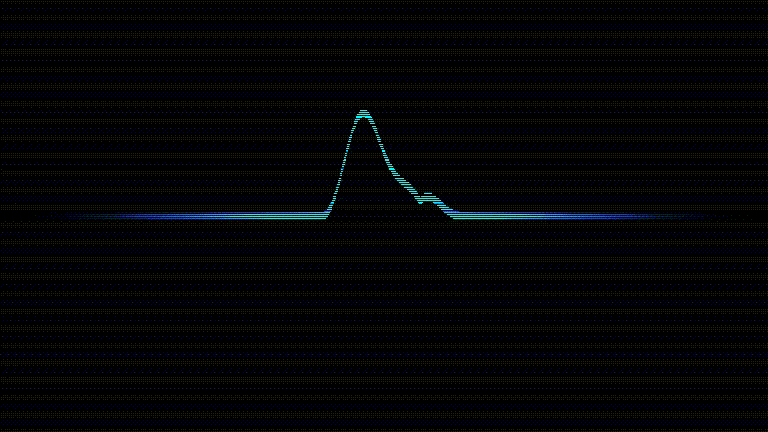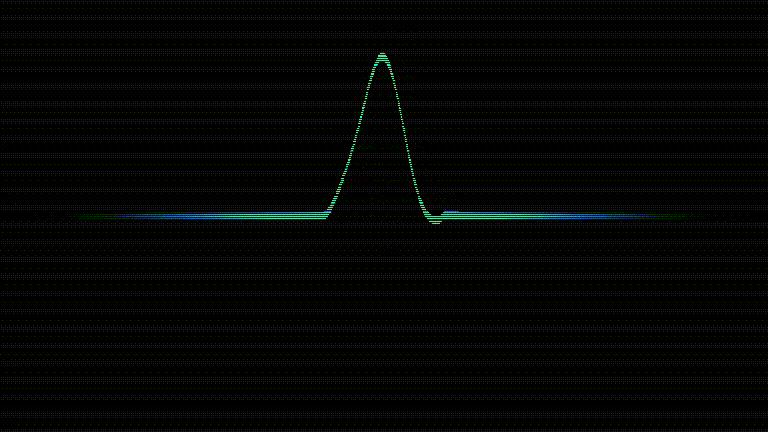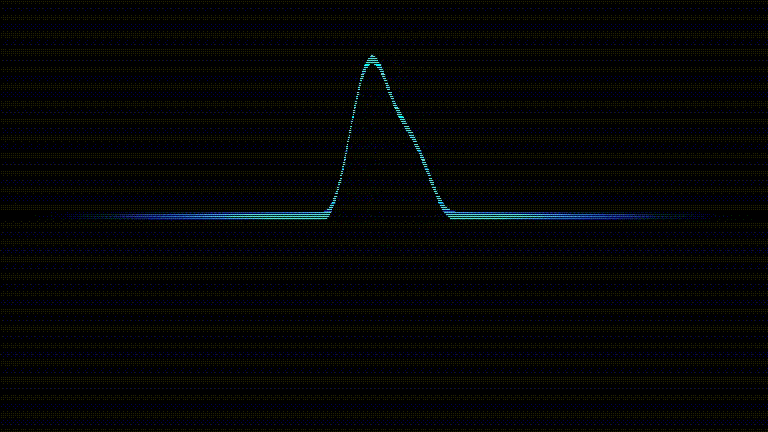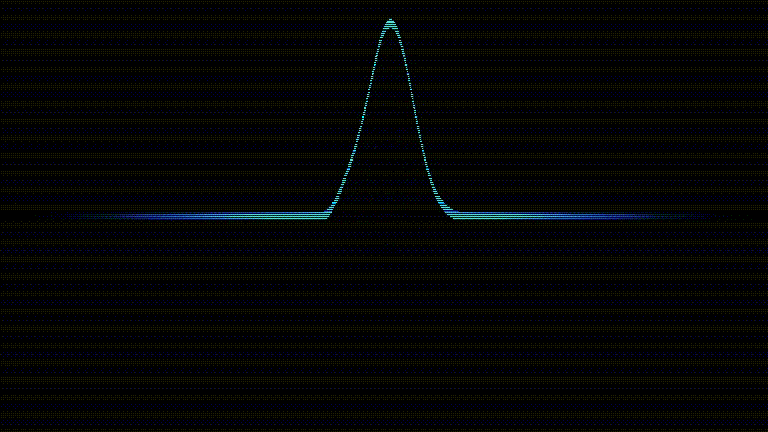
Screenshot

Méthode

Avec un langage plus classique, pour dessiner ce genre de courbe la méthode suivie aurait probablement d’implémenter une application de type : $$f_t : \mathbb{R} \rightarrow \mathbb{R}$$

Pour chacune des abscisses, on aurait calulé l’ordonnée correspondante (en prenant en compte la dimension temporelle pour le mouvement), et relier les points. Avec un fragment shader c’est un peu différent. Le shader étant calculé pour chacun des pixels issus de l’interpolation (rasterization) des primitives (voir le pipeline de rendu) la méthode “classique” n’est pas applicable. Dans notre cas, le shader est calulé pour chacun des pixel de l’image. Il s’agit donc d’obtenir une courbe depuis une fonction de type : $$f_t : \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$$

La méthode choisie ici est la suivante : à chaque point du plan (chaque pixel), on associe une couleur qui est fonction de sa distance à la courbe qu’on souhaite générer. En pratique les étapes sont:

créer le signal représenté à l’aide de fonctions mathématiques,
sélectionner la partie de la courbe qui nous intéresse,
calculer la couleur du pixel en fonction de sa distance à la courbe,
appliquer un filtre pour l’aspect “écran analogique”.

La fonction utilisée

On utilise une somme de sinusoïdes auxquelles on associe différents paramètres pour faire varier leurs aspects et la vitesse de leur mouvement. Le détail des fonctions utilisées n’a que peu d’importance. D’autres fonctions pourraient être utilisées pour un aspect plus proche de la réalité.

// Curve parameters
const float frequence = 60.0;
float phase = -3.0*iTime;

// Signal function
vec2 signal = vec2(0.0, 0.0);
signal.x = uv.x;

// 2 sinusoids
signal.y = -(0.07*(sin(frequence*signal.x+phase)))
	 + abs(0.4*(sin(frequence/5.0*signal.x+phase)));

Les coefficients du vecteur signal sont:

l’abscisse du point en cours de traitement (ramenée entre 0 et 1), et en
la valeur du signal associée à cette abscisse.

Sélection de la zone d’intéret

La fonction choisie est périodique mais on souhaite n’avoir qu’une seule impulsion (le but étant que cela ressemble à un ECG). Pour cela on aplatit les bords de la courbe.

vec2 clip(in vec2 value, in float minimum, in float maximum) {
  vec2 result = value;

  result.y *= smoothstep(minimum,0.5, value.x);
  result.y *= 1.0 - smoothstep(0.5,maximum, value.x);

  return result;
}

La fonction clip() ne conserve que les valeurs comprises entre minimum et maximum. smoothstep()` permet d’amortir la liaison entre les différentes parties de la courbe.

Attribution de la couleur

On colorie les points suffisamment proches (selon THICKNESS) de la courbe, le reste est noir.

// Fragment value is the distance between the fragment and the signal
if (distance(uv, signal) < THICKNESS)
  color = blue*intensity.y;
else
  color = black;

L’intensité (la luminosité) est fonction de l’abscisse : faible aux extrémités, forte au centre.

// Intensity decreases at the borders
vec2 intensity = vec2(uv.x, max(1.0/abs(0.5-uv.x), 1.0));
intensity = clip(intensity, 0.01, 0.99);

La fonction clip() est à nouveau utilisée ici pour éteindre les extrémités en douceur.

Aspect viel écran

On simule l’effet lignes de balayage avec l’application d’une sinusoïde de haute fréquence sur l’ensemble de la zone :

void analogic_screen_filter(inout vec3 color, in vec2 frag) {
  color *= sin(1200.0*frag.y);
}

Conclusion

Le code complet est disponible ici, et est executable sur le site Shader Toy.

Pierre Lefebvre