Les quadtrees pour les collisions en 2D
On se propose d’implémenter (C++ et SFML) une structure d’arbre quaternaire (quadtree) pour détecter les collisions d’un ensemble d’objets.
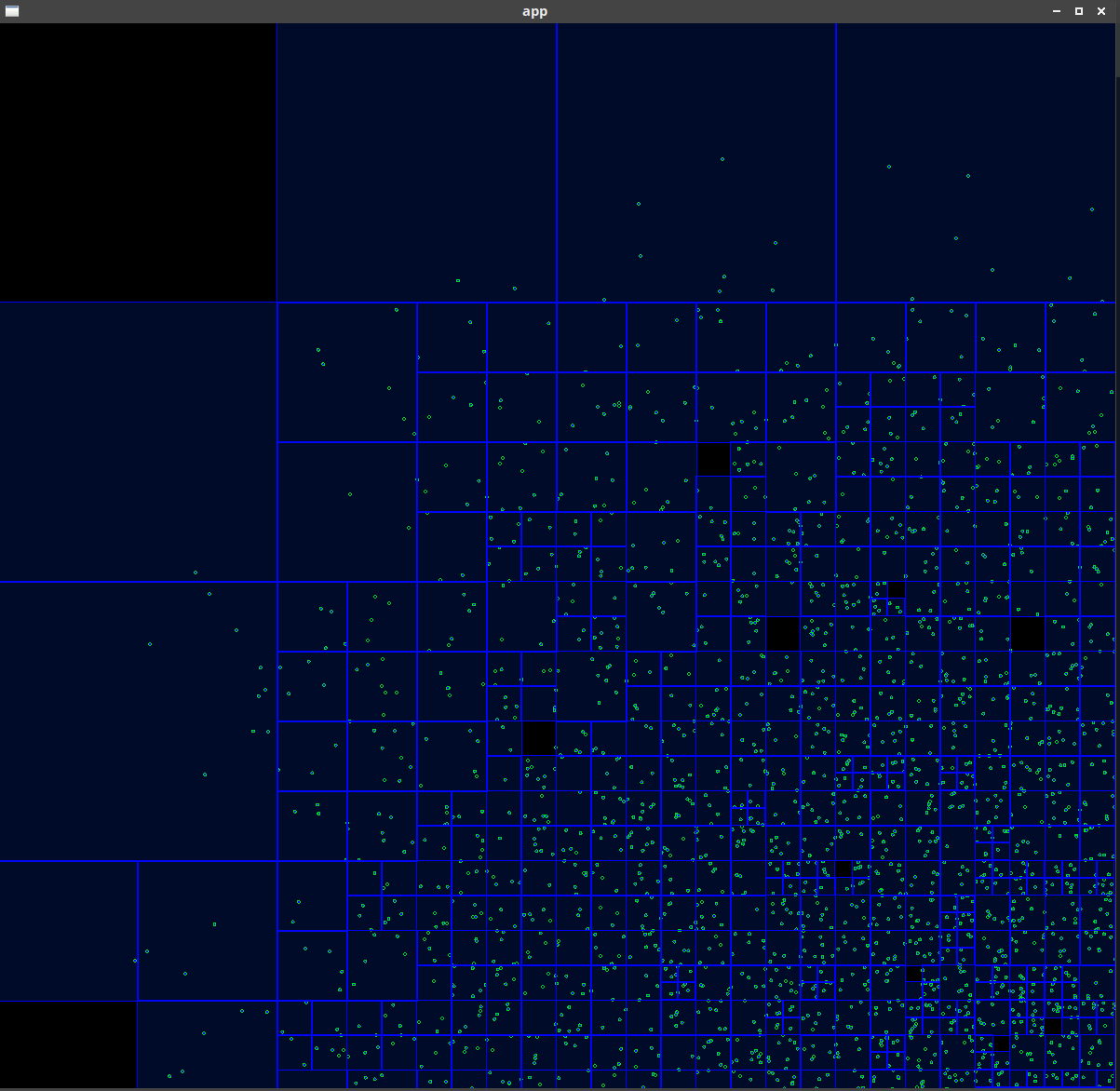
Le résultat final ressemble à ça:

Le code de ce qui est décrit ici est disponible sur le dépôt sfml-quadtree-collision.
Contexte
On considère un ensemble d’objets pouvant se déplacer, et on souhaite pouvoir mettre à jour les leurs trajectoires en fonction des éventuelles collisions qui se produisent entre ces objets.
Méthodes naïves
La méthode naïve qui vient à l’esprit pour tester les collisions entre N objets consisterait à tester toutes les collisions possibles entre tous les objets pris deux à deux. Évidemment dans le cas d’un nombre important d’objets la complexité est d’au moins O(N²) (au minimum 1 000 000 tests pour N=1000), à laquelle il faut rajouter l’éventuelle complexité de la fonction qui teste les collisions. Cette méthode trouve donc rapidement ses limites.
Pour limiter les calculs effectués, il est assez intuitif de penser qu’on pourrait ne tester que les collisions entre des objets “proches”, qui appartiennent au même voisinage. Par exemple, si un objet se trouve sur la moitié droite de l’écran, il serait judicieux de ne tester que les objets qui se trouvent également dans cette même moitié. Pour ça on pourrait maintenir une liste qui contient les objets triés de façon croissante selon leur abscisse, et reprendre l’algorithme précédent en s’arrêtant lorsque que l’on dépasse la moitié de l’écran. Si dans ce cas on économise les calculs de la fonction de collision sur un partie des objets, on en rajoute pour le tri, pour finalement avoir une complexité au pire des cas qui reste identique à celle de la méthode précédente.
Arbres quaternaires
Creusons un peu l’idée de placer les objets dans une structure de données pour les sélectionner plus rapidement. Il faudrait que cette structure permette de placer et d’accéder à chaque objet rapidement, et que la position de l’objet dans la structure permettent de localiser l’objet sur une région plus ou moins grande de l’écran. On pourrait ainsi ne tester que les collisions intervenant entre les objets d’une même région. Plus la région est petite, moins il y a d’objets à l’intérieur, et plus on économise en calcul.
C’est le but des arbres quaternaire. Il s’agit d’un arbre de recherche pour des données en deux dimensions (la position des objets), analogue aux arbres binaires de recherche pour les données en dimension 1 (les nombres). Là où pour les arbres binaires on sépare l’intervalle de recherche en deux ("plus grand que", “plus petit que”), on le divise en quatre pour les arbres quaternaires : en haut à droite, en haut à gauche, en bas à droite, en bas à gauche.
Concrètement, l’écran complet représente la racine de l’arbre (il contient tous les objets). À cette racine on relie quatre nœuds, correspondants chacun à un des quarts de l’écran, auquels on associe les objets de son parent. Pour raffiner la zone de recherche, on peut rediviser récursivement chacun des nœuds en quatre autre nœuds correspondant chacun à un seizième de l’écran, puis un soixante-quatrième d’écran, et ainsi de suite. À chaque itération on construit cet arbre en y plaçant chaque objet dans le bon nœud selon sa position. Un fois fait, chaque feuille de l’arbre constitue une région plus ou moins grande dans laquelle se trouve quelques uns de nos objets, en nombre bien inférieur au nombre total, nous donnant ainsi un ensemble d’objets à tester pour les collisions.
Pour l’exemple qui suit, les objets sont des cercles, chaque déplacement se fait en ligne droite selon un vecteur vitesse initial aléatoire, et les déplacements sont bornés aux dimensions de la fenêtre. La fonction qui teste la collision entre deux objets et la distance euclidienne élevée au carré (pour éviter la racine) entre les centres des objets.
Implémentation d’un arbre quaternaire
Dans la suite on propose une implémentation d’un arbre quaternaire. Seules les fonctions importantes sont exposées ici, pour plus de détails voir le code complet.
Les nœuds
Les informations contenues dans un nœud sont les suivantes:
- une structure de données décrivant un rectangle pour définir la région de l’écran associée au nœud (dans l’exemple, la structure est basée sur la classe
sf::Rectde la SFML); - un tableau référençant (via un identifiant) les objets contenus dans le nœud;
- un drapeau indiquant si le nœud est une feuille (valeur par défaut) ou non.
Node(const Rectangle& r):_area(r), _elements(), _leaf(true) {
for (auto& node: _nodes)
node = nullptr;
}
💡 Optimisation: Il est possible de réduire la quantité de données contenue dans un nœud, notamment pour économiser du cache de données, voir le sujet sur Stackoverflow.
Les méthodes
Ajouter un élément dans l’arbre
On peut diviser l’insertion d’un objet en deux cas :
- l’insertion dans un nœud non terminal,
- l’insertion dans un nœud terminal (une feuille).
Choix de l’enfant
Pour le premier cas, en partant de la racine l’objet doit descendre jusqu’en bas de l’arbre en sélectionnant à chaque fois le bon enfant selon sa position. Cette étape de sélection est réalisée par la méthode suivante:
template<typename T>
void insertInSubnodes(const T* entities, EntityId id) {
// Get the object positions
const Position& position = entities[id].getPosition();
// Search for the correct children for the node to be inserted
for (auto node: _nodes)
if (node->contains(position))
node->add(entities, id);
}
On teste selon la position de l’objet dans lequel des 4 enfants on doit l’insérer.
Insertion dans un nœud intermédiaire
Une fois l’enfant sélectionné (ou si le nœud est terminal), on peut insérer l’objet parmi les autres objets référencés par le nœud (tableau _elements).
Si le nombre d’objets dans un nœud devient trop grand, on raffine l’arbre en créant de nouveaux enfants pour ce nœud (voir le paragraphe suivant), et on redistribue ses objets vers ses enfants.
template<typename T>
void add(const T* entities, EntityId id) {
// If this is not a leaf, object should be inserted in the correct child
if (not _isLeaf)
insertInSubnodes<T>(entities, id);
// And if this node is a leaf, object is inserted
else {
_elements.push_back(id);
// If there is too much objects in the same node...
if (_elements.size() >= MAX_ELEMENTS) {
// ...the node is split in 4...
_split();
// ...and its elements are re-dispatched in its children
for (auto id: _elements)
insertInSubnodes<T>(entities, id);
_elements.clear();
}
}
}
Diviser un nœud avec split()
La méthode split() permet de créer les quatres enfants d’un nœuds en allouant la mémoire et en associant la zone de l’écran correspondante à ces enfants. Les nouveaux nœuds créés sont des feuilles, tandis que leur parent redevient un nœud intermédiaire.
void _split() {
// Get the area coordinates
int x = _area.left;
int y = _area.top;
int width = _area.width;
int height = _area.height;
// Create children nodes
_nodes[NORTH_WEST] = new Node(Rectangle(x, y, width/2, height/2));
_nodes[NORTH_EAST] = new Node(Rectangle(x + width/2, y, width/2, height/2));
_nodes[SOUTH_WEST] = new Node(Rectangle(x, y + height/2, width/2, height/2));
_nodes[SOUTH_EAST] = new Node(Rectangle(x + width/2, y + height/2, width/2, height/2));
// This node is no more a leaf
_isLeaf = false;
}
💡 Optimisation: N’allouer que les enfants utiles.
Nettoyage de l’arbre clear()
La suppression des nœuds se fait simplement par un parcours en profondeur de l’arbre. On descend jusqu’en bas et on libère chaque nœud en remontant. Lorsque tous les enfants d’un nœud sont supprimés, ce nœud redevient une feuille.
void clear() {
for (auto& node: _nodes)
// Depth-first search for non-null nodes
if (node != nullptr) {
node->clear();
delete node;
}
// As this node does not have children anymore, it becomes a leaf
_leaf = true;
}
💡 Optimisation: Le cas où un nœud est libéré pour être immédiatement réalloué à l’itération suivante se produit. On pourrait mettre plus d’intelligence dans la méthode clear() pour éviter que cela se produise, voir le sujet sur Stackoverflow.
Utilisation
Comme évoqué au début de l’article, l’utilisation de l’arbre de fait de la manière suivante:
- Nettoyer l’arbre;
- Mettre à jour la positions des objets;
- Ranger tous les objets dans l’arbre;
- Récupérer les feuilles;
- Tester les collisions pour les objets à l’intérieur de chaque feuille.
Ces opérations sont répétées pour chaque image affichée. Les étapes (1) et (3) ont été abordées plus haut, l’étape (2) est dépendante du programme écrit (ici, déplacement en ligne droite) et sera laissée de côté.
Récupérer les feuilles
Pour récupérer les feuilles on parcourt l’arbre en profondeur, et on stocke les feuilles rencontrées au fur et à mesure:
void getLeaves(std::vector<Node*>* out) {
// If this node is a leaf, add it to the result...
if (_isLeaf)
out->push_back(this);
// ...else scan its children
else for (auto& node: _nodes)
if (node != nullptr)
node->getLeaves(out);
}
💡 Optimisation: Pour éviter les surcoûts liés à l’utilisation de std::vector<T>, il est possible d’utiliser un tableau à taille fixe puisque le nombre maximum d’éléments contenus dans une feuille est connu.
Tester les collisions
Les objets, de type Entity, sont contenus dans le tableau _entities. Ils disposent des méthodes isColliding() et bounce() qui ne seront pas détaillées ici, et qui permettent respectivement de détecter une collision et de rebondir en cas de collision.
Les objets étant rangés dans l’arbre selon leur position, il est maintenant possible de tester les collisions entre les objets à l’intérieur des feuilles.
Les méthode isColliding() et bounce()
void App::resolveCollisions() {
// Retrieve all leaves from the quadtree
std::vector<Node*> leaves;
_quadtree->getLeaves(&leaves);
// For each leaf...
for (auto leaf: leaves) {
// ... get the associated objects
unsigned int* elements;
unsigned int nbEntities = leaf->getElements(&elements);
// Test collision between all objects in the leaf
for (unsigned int i=0; i<nbEntities; i++) {
Entity& e = _entities[elements[i]];
for (unsigned int j=i+1; j<nbEntities; j++) {
Entity& f = _entities[elements[j]];
if (e.isColliding(f)) {
e.bounce(f);
f.bounce(e);
}
}
}
}
}
Conclusion
L’implémentation d’arbres quaternaires requiert un effort d’implémentation mais permet de réduire considérablement la quantité de calculs effectuées dans le cas de la détection de collisions. L’aspect complexité algorithmique liée aux arbres quaternaires ne sera pas abordée ici, d’autres articles plus poussés existent sur le sujet.