Modélisation tumorale
Ce travail avait été réalisé pendant mes études, où j’avais été suivi par Angélique Stéphanou, chargée de Recherche en biologie computationnelle au CNRS. Je n’ai produit que le code pour la simulation et la modéle du vaisseau.
Le but était de réaliser une modélisation de la croissance d’une tumeur cancéreuse. La première partie se concentre sur un modèle de croissance simple, sans vascularisation. La seconde y ajoute un facteur de croissance permettant la création d’un réseau vasculaire (angiogénèse) qui alimente la tumeur. La modélisation utilise la méthode des éléments finis.
Modèle de tumeur non vascularisée
On modélise le comportement de chaque cellule qui peut transiter entre plusieurs états.
Automate cellulaire
Les changements d’état sont conditionnés par la quantité locale d’oxygène et la densité locale de cellules (place disponible). Les états possibles pour une cellule sont les suivants:
- Proliférative : la cellule est en mesure de se multiplier car la densité celullaire est suffisamment faible, et son apport en oxygème suffisamment élevé;
- Quiescente : l’apport en oxygène est amoindri ou la densité locale cellulaire et trop élevée, la cellule est toujours vivante mais ne se reproduit pas;
- Hypoxie : la cellule manque d’oxygène, elle libère dans son environnement un Facteur de Croissance Endothélial Vasculaire (VEGF) pour favoriser la croissance des vaisseaux sanguins aux alentours;
- Nécrose : la cellule a manqué d’oxygène trop longtemps et elle est meurt.
L’automate cellulaire est representé ci-dessous:
Profil d’oxygène
Consommation de la cellule
Dans le modèle, on considére qu’une cellule consomme l’oxygène uniquement de la maille où elle se trouve. On utilise la loi de Michaelis-Menten pour représenter la consommation d’oxygène :
$$Q_{\text{absorbée}} = Q_{\text{max}} \cdot \frac{{Q(i,j)}}{{K + Q(i,j)}}$$
avec \(Q(i,j)\) la quantité d’oxygène disponible au point \((i,j)\).
Diffusion de l’oxygène dans le milieu
Pour connaître la quantité d’oxygène \(O: (x,y,t) \in \mathbb{R}^3 \rightarrow O(x,y,t) \in \mathbb{R}\) en chaque point on résoud à chaque instant \(t\) l’équation de diffusion, avec \(D\) le coefficient de diffusion :
$$\frac{\partial O}{\partial t} = D \nabla^2 O = D \left(\frac{\partial^2 O}{\partial x^2} + \frac{\partial^2 O}{\partial y^2}\right)$$
Pour toute fonction \(f : x \in \mathbb{R} \rightarrow f(x) \in \mathbb{R}\) avec \(f~C^2\), le théroème de Taylor-Young nous donne :
$$f(x+h) = f(x) + h \cdot \frac{df}{dx}(x) + h^2 \cdot \frac{d^2 f}{dx^2}(x) + o(h^2)~(1)$$ $$f(x-h) = f(x) - h \cdot \frac{df}{dx}(x) + h^2 \cdot \frac{d^2 f}{dx^2}(x) + o(h^2)~(2)$$
La combinaison \((1) - (2)\) nous donne :
$$f’(x) = \frac{f(x+h) - f(x-h)}{2 \cdot h}$$ $$f’’(x) = \frac{f(x+h) + f(x-h) - 2 \cdot f(x)}{h^2}$$
En discrétisant et en appliquant à \(O\) on obtient:
$$\frac{{\partial O}}{{\partial t}}(x,y,t) = \frac{{O(x,y,t+\Delta t) - O(x,y,t-\Delta t)}}{{2 \cdot \Delta t}}$$ $$\frac{{\partial^2 O}}{{\partial x}^2}(x,y,t) = \frac{{O(x+\Delta x,y,t) + O(x-\Delta x,y,t) - 2 \cdot O(x,y,t)}}{{\Delta x}^2}$$ $$\frac{{\partial^2 O}}{{\partial y}^2}(x,y,t) = \frac{{O(x,y+\Delta y,t) + O(x,y-\Delta y,t) - 2 \cdot O(x,y,t)}}{{\Delta y}^2}$$
L’équation de diffusion discrétisée devient donc :
$$O_{i,j}^{t+1} = \frac{D \Delta t}{\Delta x^2} \cdot (O^t_{i+1,j} + O^t_{i-1,j} + O^t_{i,j+1} + O^t_{i,j-1}) + O^t_{i,j} \cdot \left(1 - 4 \frac{D \Delta t}{\Delta x}\right)$$
Simulation
De gauche à droite:
- départ de croissance,
- début de l’hypoxie au centre,
- formation du coeur nécrotique,
- fin de prolifération,
- hypoxie généralisée,
- nécrose totale par hypoxie.
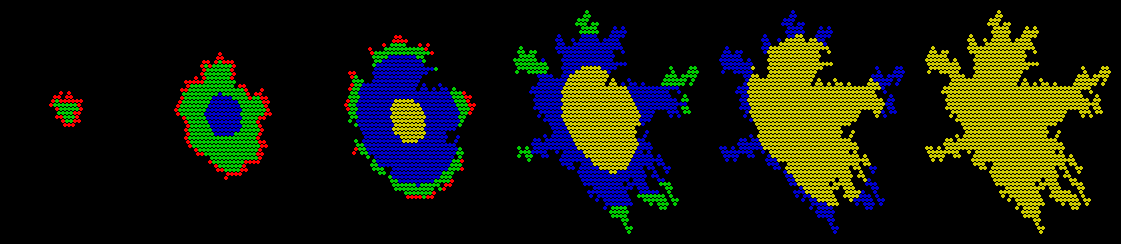
Angiogénèse et réseau vasculaire
La libération du facteur de croissance endothélial par les cellules peut entraîner une vascularisation de la tumeur, et modifier sa croissance.
Facteur de croissance
La sécrétion du VEGF par les cellules hypoxiques peut guider la création de nouveaux vaisseaux sanguins qui vont venir alimenter la tumeur. Son apport en oxygène se trouve renforcé, et peut permettre une reprise de croissance.
Le facteur de croissance suit la même loi de diffusion que l’oxygène, et la croissance des vaisseaux est guidée par le gradient de densité de celui-ci. Les vaisseaux se dirigeront vers les fortes concentrations de VEGF.
Modélisation des vaisseaux
Les vaisseaux sanguins sont modélisès par un arbre binaire:
type Vessel = None
| Leaf of (int*int*int*bool)
| Node of (int*int*int*bool)*Vessel*Vessel;
Chaque étiquette contenant:
- la position du vaisseau,
- son épaisseur,
- son activité (actif ou non).
À chaque incrément, pour chaque extrémité active, on va vérifier la place disponible, relever la direction du gradient de VEGF, relever la concentration en VEGF, ajouter un branchement et diminuer l’épaisseur du vaisseau. La présence de vaisseau sur une maille se traduit par un apport d’oxygène, inversemment proportionnel à l’épaisseur du vaisseau.
Simulation
De gauche à droite:
- départ de croissance,
- hypoxie et sécrétion de VEGF,
- ralentissement de prolifération,
- création de nouveaux vaisseaux,
- réoxygènation progressive,
- poursuite de croissance.

Conclusion
Les travaux de recherche à ce sujet sont toujours en cours. À ma connaissance, le modèle ajoute aujourd’hui une 3e dimension, et des caractéristiques sur la géométrie des cellules ainsi que des propriètés de leur membrane.


